bart rss

=========================================================================================================================

The bart rss command is used in BART is used to compute the Root Sum of Squares (RSS): a mathematical technique used to combine multiple values by calculating the square root of the sum of their squared values. It is often used in situations where you need to compute the magnitude of a combined set of values.

Where we can view the full usage string and optional arguments with the -h flag.

How bart rss Works

The Root Sum of Squares calculation combines data from different coils using the following formula:

\[{RSS} = \sqrt{\sum_{i \in D}^{N} |S_i|^2} \]

where:

• \(S_i\) represents the i’th element of the signal,

• \( N \) is the dimension size

• The absolute value (magnitude) of the signal is squared, summed across all elements, and then the square root of the sum is taken.

This is equivalent to taking the \(\ell_2\)-norm along a specific dimension

!bart rss -h

Usage: rss bitmask <input> <output> 

Calculates root of sum of squares along selected dimensions.

-h  help

where:

bitmask: A bitmask to specify the dimensions along which to perform the Root Sum of Squares.

<input>: The file containing the input data.

<output>: The file where the combined RSS result will be saved.

Example for Matrix (using Bash)

Create a Matrix Filled with the Value of 1, Dimension as 2 x 4 x 2

!bart ones 3 2 4 2 matrix 

!bart show matrix # Display the matrix

+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i
+1.000000e+00+0.000000e+00i	+1.000000e+00+0.000000e+00i

Example 1.1

Calculates the Rss Across a 0th Dimension and Named as matrix_1

!bart rss $(bart bitmask 0) matrix matrix_1

!bart show matrix_1

+1.414214e+00+0.000000e+00i	+1.414214e+00+0.000000e+00i	+1.414214e+00+0.000000e+00i	+1.414214e+00+0.000000e+00i
+1.414214e+00+0.000000e+00i	+1.414214e+00+0.000000e+00i	+1.414214e+00+0.000000e+00i	+1.414214e+00+0.000000e+00i

We can see the dimension for our new matrix (matrix_1) become 1 x 4 x 2

!bart show -m matrix_1

Type: complex float
Dimensions: 16
AoD:	1	4	2	1	1	1	1	1	1	1	1	1	1	1	1	1

Example 1.2

Continue to Calculate rss for Matrix_1 along Demension 2

!bart rss $(bart bitmask 2) matrix_1 matrix_2

!bart show matrix_2

+2.000000e+00+0.000000e+00i	+2.000000e+00+0.000000e+00i	+2.000000e+00+0.000000e+00i	+2.000000e+00+0.000000e+00i

!bart show -m matrix_2

Type: complex float
Dimensions: 16
AoD:	1	4	1	1	1	1	1	1	1	1	1	1	1	1	1	1

Example 1.3

Calculate the Root Sum of Squares (RSS) Across all Dimensions of a Matrix using BART

!bart rss $(bart bitmask 0 1 2) matrix matrix_3

!bart show matrix_3

+4.000000e+00+0.000000e+00i

!bart show -m matrix_3

Type: complex float
Dimensions: 16
AoD:	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

Example Workflow for Images (in Python)

The bart rss command in BART is often used to calculate the Root Sum of Squares (RSS) across specified dimensions of multi-coil MRI data. This operation is commonly used to combine data from different coils into a single image, enhancing the signal-to-noise ratio (SNR).

# Importing the required libraries
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import cfl
from bart import bart

1. Generate a multi-coil image using the phantom simulation tool in BART:

Generate a multi-coil image with size 128x128 and 8 coils.
Note the convention is that the coil dimension is dimension 3

multi_coil_image = bart(1, 'phantom -x 128 -s 8')
print(multi_coil_image.shape)

(128, 128, 1, 8)

# Visualizing the multi-coil images using Matplotlib 
plt.figure(figsize=(16,20))
for i in range(8):
    plt.subplot(1, 8, i+1)
    plt.imshow(abs(multi_coil_image[...,i]), cmap='gray')
    plt.title('Coil image {}'.format(i))

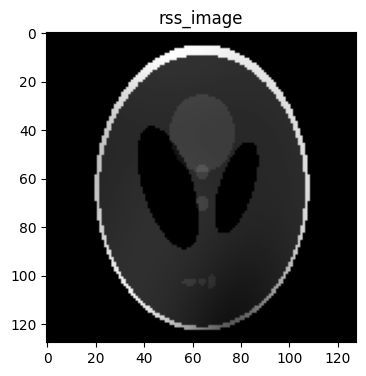
2. Combine the Coil Images Using rss :

The number of coils is located in dimension 3, and the corresponding bitmask for dimension 3 is calculated to be 8

!bart bitmask 3

8

rss_image = bart(1, 'rss 8', multi_coil_image) # Calculates the rss across coil dimension and named as rss_image

# Visualizing the rss_image using Matplotlib
plt.figure(figsize=(4,6))
plt.imshow(abs(rss_image), cmap='gray')
plt.title('rss_image')

Text(0.5, 1.0, 'rss_image')