bart avg

bart avg#

===========================================================================================================

The bart avg command is used to average along a specific dimension of multi-dimensional arrays using a bitmask.

Where we can view the full usage string and optional arguments with the -h flag.

How bart avg Works#

The averaging process computes the mean value along the specified dimension(s). If you want to average over a given dimension, the formula is:

\[{Average} = \frac{1}{N} {\sum_{i=1}^{N} x_i} \]

where:

  • \(N\) is the number of elements along the dimension to be averaged.

  • \(x_i\) represents the individual data points in the dimension being averaged.

!bart avg -h

Usage: avg [-w] bitmask <input> <output> 

Calculates (weighted) average along dimensions specified by bitmask.

-w    weighted average
-h    help

Where:

-w: This option enables weighted averaging.

bitmask: A bitmask to specify the dimensions along which to perform the averaging.

<input>: The input .cfl file.

<output>: The output .cfl file containing the averaged data.

Example for Matrix (using Bash)#

Create a Matrix, Dimension as 2 x 2 x 2#

!bart vec $(seq 1 8) array # Generate a array with values from 1 to 8 

!bart show array

+1.000000e+00+0.000000e+00i	+2.000000e+00+0.000000e+00i	+3.000000e+00+0.000000e+00i	+4.000000e+00+0.000000e+00i	+5.000000e+00+0.000000e+00i	+6.000000e+00+0.000000e+00i	+7.000000e+00+0.000000e+00i	+8.000000e+00+0.000000e+00i

!bart reshape $(bart bitmask 0 1 2) 2 2 2 array matrix_array # Reshape the array to Dimension as 2 x 2 x 2

!bart show matrix_array

+1.000000e+00+0.000000e+00i	+2.000000e+00+0.000000e+00i
+3.000000e+00+0.000000e+00i	+4.000000e+00+0.000000e+00i
+5.000000e+00+0.000000e+00i	+6.000000e+00+0.000000e+00i
+7.000000e+00+0.000000e+00i	+8.000000e+00+0.000000e+00i

!bart show -m matrix_array

Type: complex float
Dimensions: 16
AoD:	2	2	2	1	1	1	1	1	1	1	1	1	1	1	1	1

Example 1.1#

Calculated the Average Along a Dimension “0” of the matrix_array#

!bart avg $(bart bitmask 0) matrix_array matrix1_array

!bart show matrix1_array

+1.500000e+00+0.000000e+00i	+3.500000e+00+0.000000e+00i
+5.500000e+00+0.000000e+00i	+7.500000e+00+0.000000e+00i

We can see the dimension for our new matrix (matrix1_array) become 1 x 2 x 2

!bart show -m matrix1_array

Type: complex float
Dimensions: 16
AoD:	1	2	2	1	1	1	1	1	1	1	1	1	1	1	1	1

Example 1.2#

Continue to Calculate avg for matrix1_arry along Demension “2”#

!bart avg $(bart bitmask 2) matrix1_array matrix2_array

!bart show matrix2_array

+3.500000e+00+0.000000e+00i	+5.500000e+00+0.000000e+00i

!bart show -m matrix2_array

Type: complex float
Dimensions: 16
AoD:	1	2	1	1	1	1	1	1	1	1	1	1	1	1	1	1

Example 1.3#

Calculate the avg Across all Dimensions of a Matrix using BART#

!bart avg $(bart bitmask 0 1 2) matrix_array matrix3_array

!bart show matrix3_array

+4.500000e+00+0.000000e+00i

!bart show -m matrix3_array

Type: complex float
Dimensions: 16
AoD:	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1

Example Workflow for Images (in Python Kernel)#

The bart avg command in BART is often used to calculate the Average data across one or more specified dimensions. It is typically employed in cases where multi-dimensional data, such as MRI data, needs to be averaged along specific axes, such as repetitions, coils, or slices.

Example in Coils#

# Importing the required libraries
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

import cfl
from bart import bart

1. Generate a multi-coil image using the phantom simulation tool in BART:#

Generate a multi-coil image with size 128x128 and 8 coils.
Note the convention is that the coil dimension is dimension 3

# Generate a multi-coil image with size 128x128 and 8 coils
multi_coil_image = bart(1, 'phantom -x 128 -s 8')
print(multi_coil_image.shape)

(128, 128, 1, 8)

# Visualizing the multi-coil images using Matplotlib 
plt.figure(figsize=(16,20))
for i in range(8):
    plt.subplot(1, 8, i+1)
    plt.imshow(abs(multi_coil_image[...,i]), cmap='gray')
    plt.title('Coil image {}'.format(i))
_images/cf601ddc3d286bdddc2abb855cfa494dcaadaf15bfe077ce083f948ef231587a.png

2. Combine the Coil Images Using avg :#

The number of coils is located in dimension 3, and the corresponding bitmask for dimension 3 is calculated to be 8

!bart bitmask 3

8

avg_image = bart(1, 'avg 8', multi_coil_image) # Calculates the avg across coil dimension and named as avg_image

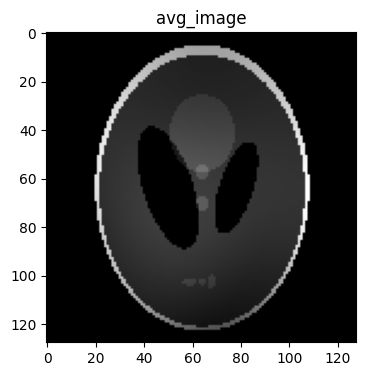
# Visualizing the avg_image using Matplotlib
plt.figure(figsize=(4,6))
plt.imshow(abs(avg_image), cmap='gray')
plt.title('avg_image')

Text(0.5, 1.0, 'avg_image')
_images/03e2b18b2b3327d4cf1fc5a51d79254bd4b27eb377291132ff968f3f24199570.png
Contents